TEMA 3. Teorema de la probabilidad total

En teoría de la probabilidad, el teorema de la probabilidad total es una ley que permite calcular la probabilidad de un suceso que no forma parte de un espacio muestral a partir de las probabilidades condicionales de todos los sucesos de dicho espacio muestral.

Así pues, el teorema de la probabilidad total sirve para calcular la probabilidad de un suceso específico a partir de información parcial sobre ese suceso. A veces no podemos determinar la probabilidad de un suceso aplicando directamente la regla de Laplace, ya que no tenemos toda la información necesaria. Pero si conocemos datos de dicho suceso relativos a otros eventos, el teorema de la probabilidad total suele ser útil.

En definitiva, el teorema de la probabilidad total se usa cuando queremos calcular la probabilidad de un suceso, pero solo se tiene información sobre él en ciertas condiciones.

 

Fórmula del teorema de la probabilidad total

El teorema de la probabilidad total dice que dado un conjunto de sucesos {A₁, A₂,…, A_n} que forman una partición sobre el espacio muestral, la probabilidad del evento B es igual al sumatorio de los productos de la probabilidad de cada suceso P(A_i) por la probabilidad condicional P(B|A_i).

Por lo tanto, la fórmula del teorema de la probabilidad total es la siguiente:

 

Donde:

• es la probabilidad de que ocurra el suceso B.
• es la probabilidad condicional del suceso B dado el suceso A_i.
• es la probabilidad de que ocurra el suceso A_i.

Ten en cuenta que en probabilidad una partición del espacio muestral se define como un conjunto de sucesos incompatibles entre sí cuya unión forma el espacio muestral.

Ejemplo

• Una tienda de electrónica vende tres marcas de televisores: X, Y, Z. Se estima que el 20% de las ventas son televisores de la marca X, el 50% de la marca Y y el 30% de la marca Z. El 5% de los televisores de la marca X son defectuosos, el 3% de los televisores de la marca Y son defectuosos y el 4% de los televisores de la marca Z son defectuosos. ¿Cuál es la probabilidad de comprar un televisor defectuoso?

El enunciado del problema nos da las probabilidades de que un cliente compre cada marca de televisores:

• Suceso A₁: Un cliente compra un televisor de la marca X → P(A₁)=0,20
• Suceso A₂: Un cliente compra un televisor de la marca Y → P(A₂)=0,50
• Suceso A₃: Un cliente compra un televisor de la marca Z → P(A₃)=0,30

Además, el enunciado del ejercicio también nos proporciona la probabilidad que un televisor sea defectuoso de cada marca:

Suceso B: El televisor es defectuoso

• B|A₁: Dado un televisor de la marca X, el televisor es defectuoso → P(B|A₁)=0,05
• B|A₂: Dado un televisor de la marca Y, el televisor es defectuoso → P(B|A₂)=0,03
• B|A₃: Dado un televisor de la marca Z, el televisor es defectuoso → P(B|A₃)=0,04

Así pues, el árbol de probabilidades del problema es el siguiente:

 

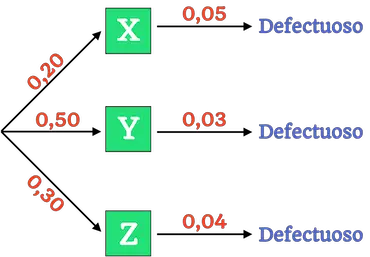
Entonces, para calcular la probabilidad de comprar un televisor defectuoso tenemos que utilizar la fórmula de la regla de la probabilidad total:

En nuestro caso, el espacio muestral está formado por tres eventos (A₁, A₂ y A₃), por lo tanto, la fórmula del teorema de la probabilidad total queda de la siguiente manera:

De modo que solo nos queda sustituir las probabilidades en la expresión anterior para hallar la probabilidad de comprar un televisor defectuoso:

En conclusión, hay una probabilidad del 3,7% de que compremos un televisor y este sea defectuoso.