TEMA 5. Combinaciones y permutaciones
Combinaciones y permutaciones
¿Qué diferencia hay?
Normalmente usamos la palabra "combinación" descuidadamente, sin pensar en si el orden de las cosas es importante. En otras palabras:
"Mi ensalada de frutas es una combinación de manzanas, uvas y bananas": no importa en qué orden pusimos las frutas, podría ser "bananas, uvas y manzanas" o "uvas, manzanas y bananas", es la misma ensalada.
"La combinación de la cerradura es 472": ahora sí importa el orden. "724" no funcionaría, ni "247". Tiene que ser exactamente 4−7−2.
Así que en matemáticas usamos un lenguaje más preciso:
- Si el orden no importa, es una combinación.
- Si el orden sí importa es una permutación.

¡Así que lo de arriba se podría llamar "cerradura de permutación"!
En otras palabras:
Una permutación es una combinación ordenada.
|
Para ayudarte a recordar, piensa en "Permutación... Posición" |
Permutaciones
Hay dos tipos de permutaciones:
- Se permite repetir: como la cerradura de arriba, podría ser "333".
- Sin repetición: por ejemplo, los tres primeros en una carrera. No puedes quedar primero y segundo a la vez
1. Permutaciones con repetición
Son las más fáciles de calcular.
Cuando una cosa tiene n tipos diferentes ... ¡tenemos n opciones cada vez!
Por ejemplo: eligiendo 3 de esas cosas, las permutaciones son:
n × n × n
(n multiplicado 3 veces)
De manera más general: eligiendo r de algo que tiene n tipos diferentes, las permutaciones son:
n × n × ... (r veces)
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)
Lo cual es más fácil de escribir usando un exponente igual a r:
n × n × ... (r veces) = nr
Ejemplo: en la cerradura de arriba, hay 10 números para elegir (0,1,2,3,4,5,6,7,8,9) y eliges 3 de ellos:
10 × 10 × ... (3 veces) = 103 = 1,000 permutaciones
Entonces, la fórmula es simplemente:
|
nr |
|
donde n es el número de cosas se pueden elegir, |
2. Permutaciones sin repetición
En este caso, se reduce el número de opciones en cada paso.
Ejemplo: ¿cómo podrías ordenar 16 bolas de billar?
Después de elegir por ejemplo la "14" no puedes elegirla otra vez.
Así que tu primera elección tiene 16 posibilidades, y tu siguiente elección tiene 15 posibilidades, después 14, 13, etc. Y el total de permutaciones sería:
16 × 15 × 14 × 13 ... = 20,922,789,888,000
Pero a lo mejor no quieres elegirlas todas, solo 3 de ellas, así que sería solamente:
16 × 15 × 14 = 3,360
Es decir, hay 3,360 maneras diferentes de elegir 3 bolas de billar de entre 16.
Sin repetición, nuestras opciones se reducen cada vez.
¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"
|
! |
La función factorial (símbolo:!) significa que se multiplican números descendentes. Ejemplos:
|
|
Nota: en general se está de acuerdo en que 0! = 1. Puede que parezca curioso que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas ecuaciones. |
|
Así que si quieres elegir todas las bolas de billar las permutaciones serían:
16! = 20,922,789,888,000
Pero si solo quieres elegir 3, tienes que dejar de multiplicar después de 14. ¿Cómo lo escribimos? ¡Hay un buen truco... dividimos entre 13!...

Eso fue genial: el 13 × 12 × ... etc. se "cancela", dejando solo 16 × 15 × 14.
La fórmula se escribe así:
|
n!(n − r)! |
|
donde n es el número de cosas que puedes elegir, |


Notación
En lugar de escribir toda la fórmula, la gente usa otras notaciones como:
P(n,r) = nPr = nPr = n!/ (n−r)!
Ejemplos:
- P(10,2) = 90
- 10P2 = 90
- 10P2 = 90
Combinaciones
También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):
- Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
- Sin repetición: como números de lotería (2,14,15,27,30,33)
1. Combinaciones con repetición
En realidad son las más difíciles de explicar, así que las dejamos para luego.
2. Combinaciones sin repetición
Así es como funcionan las loterías. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!
La manera más fácil de explicarlo es:
- imaginemos que el orden sí importa (permutaciones),
- después lo cambiamos para que el orden no importe.
Volviendo a las bolas de billar, digamos que queremos saber qué 3 bolas se eligieron, no el orden.
Ya sabemos que 3 de 16 dan 3360 permutaciones.
Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.
Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:
|
El orden importa |
El orden no importa |
|
1 2 3 |
1 2 3 |
Así que las permutaciones son 6 veces más posibilidades.
De hecho, hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:
3! = 3 × 2 × 1 = 6
(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)
Así que solo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos
(porque no nos interesa ordenarlos):

Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:
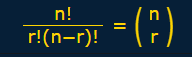
|
donde n es el número de cosas que puedes elegir, |
A menudo se le llama "n en r" (como "16 en 3")
Y también se conoce como el Coeficiente binomial.
Notación
Todas estas notaciones significan "n en r":

Solo recuerda la fórmula:

Ejemplo: Bolas de billar (sin orden)
Entonces, nuestro ejemplo de bolas de billar (ahora sin orden) es:

En conclusión:
